Chess Engine using Reinforcement Learning

Abstract

Machine learning based chess engines have always proven themselves to outperform human capabilities in the strategic field of chess. The number of possibilities after every move someone makes increases exponentially. For example, after just two moves (two turns for white and two for black), there are 197,742 possible board positions. Certain grandmasters of chess are able to see 5 to 10 moves in the future in order to decide the best move to play, but that is in exchange for the lifetime of training they devote to this world of 64 squares.

This is where computers come into play. While chess engines learn much faster and can calculate to much further depths than a human can, a perfect chess engine has still always been the biggest challenge to the world of Artificial intelligence. While the Deep Blue started making headlines in 1996, the top-level chess engines started beating human beings around the 1970s. However, needless to say, the chess engines have come a long way since then, with stockfish being the highest-rated chess engine to date, implementing supervised and unsupervised learning techniques with some pre-fed information contributed by top world grandmasters, and DeepMind’s Deep Reinforcement learning based AlphaZero, which learned to play excellent chess, even beating stockfish, entirely from self-play over a few hours of training.

The aim of our project is to create a similar chess engine, which can at least beat average-level players and is more or less self-trained, using deep reinforcement learning techniques and neural network-based algorithms. The aim is to build an AlphaZero-based chess engine implementing deep neural network architectures paired with Monte Carlo Tree Search, but at the same time diverge from AlphaZero in that we’ll avoid a full board representation and use a handcrafted feature vector instead, inspired by the Giraffe paper. We will also use Stockfish and a few other methods to accelerate training.

Literature Review

Giraffe: Using Deep Reinforcement Learning to Play Chess by Matthew Lai

NEURAL NETWORK BASED EVALUATION

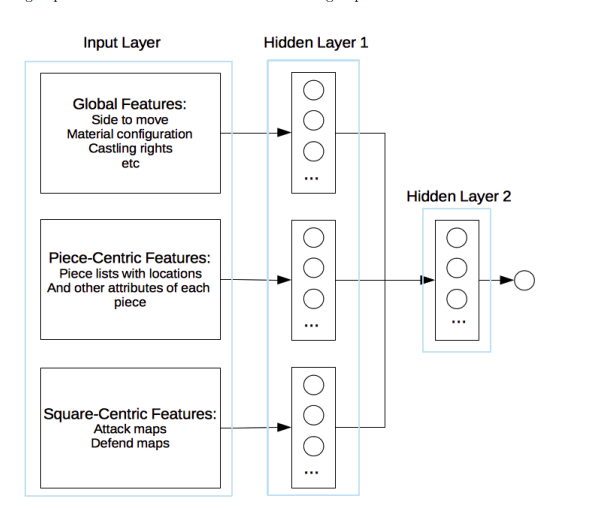
Feature Representation

• Side to Move
• Castling Rights
• Material Configuration
• Piece Lists
• Sliding Pieces Mobility
• Attack and Defend Maps

Total Features - 363

Network Architecture

Training Set Generation Approach

5 million positions randomly selected from databases and a random legal move to each position, introducing imbalances and more unusual positions.

Network Initialization

Evaluative function with only basic material knowledge used.

TD-Leaf

Implementation of TD Leaf using following update rule:

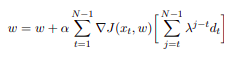
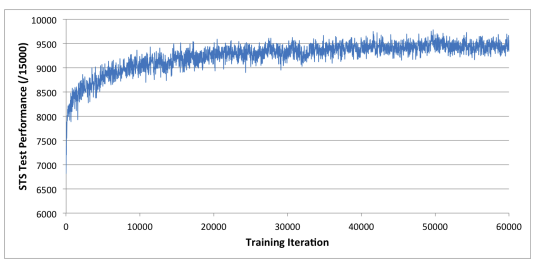
Result

PROBABILISTIC SEARCH

Limit the search based on the probability of a move being a part of the main line.

NEURAL NETWORK BASED PROBABILITY ESTIMATION

Train a neural network to give $ P(child_i|parent)$

Feature Representation

• Piece Type
• From Square
• To Square
• Promotion Type
• Rank

Network Architecture

Similar to the one used earlier.

Training Positions Generation

Time Limited Search on the root positions from the training set for the evaluation network training and randomly sample from the positions encountered as internal nodes in those searches. 5 million positions.

Network Training

Stochastic Gradient Descent with AdaDelta update rules using the cross-entropy loss function.

RESULTS AND EVALUATION

Difference is 48+-12 Elo points.

CONCLUSION

The learned system performed at least comparably to the best expert-designed counterparts in existence at the time.

Supervised and Reinforcement Learning from Observations in Reconnaissance Blind Chess by Timo Bertram, Johannes Furnkranz and Martin Muller

The paper explores how to teach an artificial intelligence (AI) agent to play the imperfect information game of reconnaissance blind chess (RBC) using the AlphaGo methodology. RBC is an imperfect information game, unlike traditional board games like chess and go, where players have little knowledge of where the opponent’s pieces are.

The research suggests a modification of the AlphaGo training method for RBC, which entails training a supervised agent on publicly accessible game records and then improving its performance through self-play using the Proximal Policy Optimisation reinforcement learning algorithm. Instead of a detailed description of the game state, the agent is trained to produce moves based on observations of the current state of the game. According to the article, using only observations is required to prevent issues brought on by the partial observability of game states in RBC.

Network Architecture

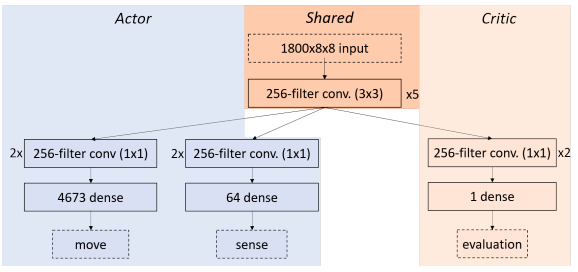
Results

The suggested strategy led to an ELO of 1330 on the RBC leaderboard, moving the agent up to position 27 at the time of writing. The outcomes show that self-play considerably enhances the agent’s performance and that the agent is capable of playing respectably without search and without assuming the genuine game state.

Reinforcement Learning in an Adaptable Chess Environment for Detecting Human-understandable Concepts

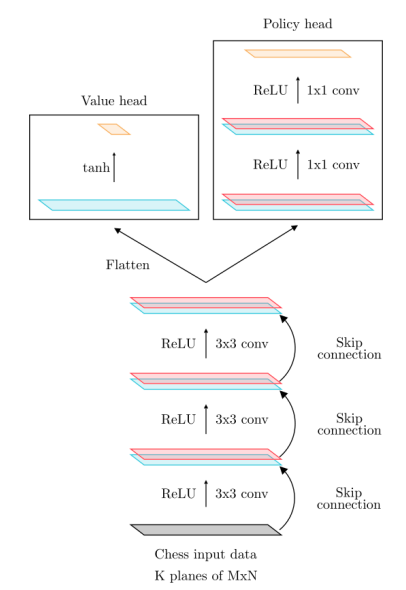
This paper aims to make the engine master the game of chess via self play. The agent is a deep neural network with randomly initialised weights, which get better as it trains by playing against itself and learns to recognise board patterns. The environment consists of a board with user defined board size, with a simple interface for extracting useful information regarding the board state. The environment is also coupled with a standard variant of Monte Carlo Tree Search (MCTS). TensorFlow Lite is utilised to provide fast neural network guidance without having to rely on batching predictions for the GPU.

Concepts are detected by learning a set of logistic probes for a data set representing the concept of interest, using the activation outputs for each intermediary layer in the neural network. The aim is to find the best-fitting logistic regressor with weights w and bias b so that

$||σ (w · Oi + b) − Pi||^2$ is minimised, where Oi are the activation outputs and Pi are the binary labels {0, 1}. Then a random sample of 10% of the data is tested for validation of the model

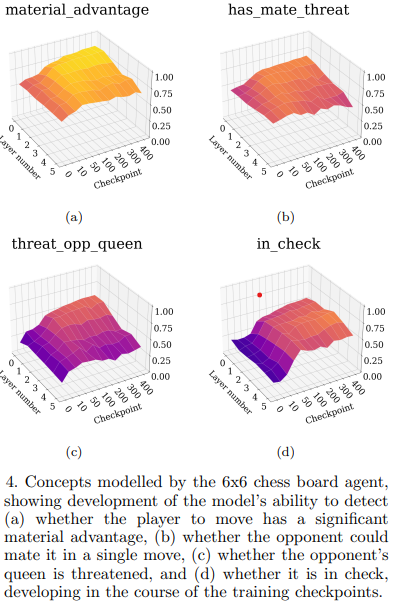
The probed concepts for the 4x5 and 6x6 agents are:

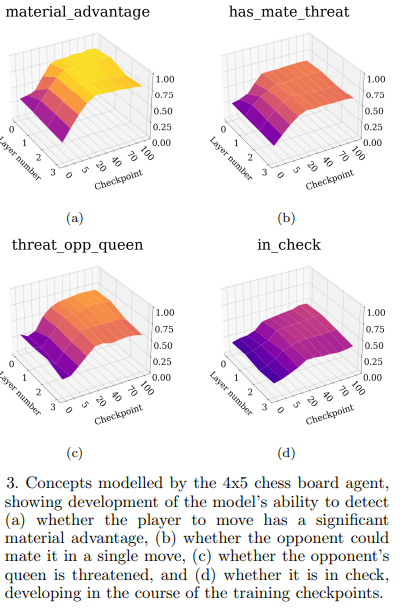
We can see that soon after in the training process, proceeding approximately 30 iterations, the 4x5-agent learns to represent whether it is threatening the opponent’s queen. . Later, after approximately 50 iterations, the agent learns to represent whether it has a potential mating attack. Surprisingly, the agent represents the state of being in check only weakly throughout the entire training process, despite learning to play optimally. All the probed concepts flatten out after about 100 training iterations, regardless of whether training continues. This indicates that this agent is highly unlikely to allocate more resources to represent these concepts provided more experience.

For the 6x6-agent, many of the same trends as the 4x5 agent can be seen, the main difference being that material advantage as well as has mate threat are detectable already at the beginning of the training loop.

In an RL context, most of the early learning takes place because the agent accidentally succeeds, i.e. delivers a checkmate. As a consequence, concepts connected to actions that are statistically more likely to win the game for a given agent, appear during the earliest stages of training.

The implementation is limited to probing for linearly represented concepts, although there are no guarantees that the network represents its knowledge in a linearly separable manner. Also, it cannot highlight the differences between being able to detect concepts and knowing how the represented concepts are utilised within the given model. For example: it is easy for a human to understand that the player holding less material is more likely to lose. However, whether or not the model has made the same connection cannot be guaranteed.

Network Architecture

Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm

The paper introduces the AlphaZero reinforcement learning method, which trains a neural network to play board games. By teaching the algorithm to play chess and shogi (Japanese chess) without prior knowledge of the game’s rules or strategies, the authors demonstrated the algorithm’s effectiveness. The system eventually attained a superhuman level of performance, outperforming the top computer and human players in each game.

The introduction to reinforcement learning, a subset of machine learning involving an agent interacting with its surroundings to learn how to complete a task, is the paper’s first section. The authors describe the AlphaZero approach, which combines a deep neural network with a Monte Carlo tree search to learn how to play a game through self-play.

The algorithm for the proposed AlphaZero was -

• The parameters of the neural network are initialized randomly
• Games are played by selecting moves for both players by MCTS
• At the end of the game, the terminal position is scored according to the rules as +1 for a win, 0 for neutral, and -1 for a loss
• Neural network parameters are updated with 2 aims
  • To minimize the error between predicted and game outcome
  • To maximize the similarity of the policy vector to the search probabilities

The author also discussed how their algorithm was different from the AlphaGo Zero algorithm

• AlphaGo Zero estimates and optimizes the probability of winning, assuming binary win/loss outcomes. AlphaZero estimates and optimizes the expected outcome, taking account of draws or potentially other outcomes
• In AlphaGo Zero, self-play games were generated by the best player from all previous iterations. AlphaZero simply maintains a single neural network that is updated continually rather than waiting for an iteration to complete
• AlphaGo Zero tuned the hyper-parameters of its search by Bayesian optimization. In alphaZero, they reuse the same hyper-parameters for all games without game-specific tuning

The writers used chess, Shogi, and Go as test cases for AlphaZero. After only a few hours of practice, the algorithm was able to master all three games at a superhuman level. The results for chess and shogi are the main subject of the paper.

The authors compared AlphaZero’s chess performance to that of Stockfish and Elmo, two more chess programs. Elmo was a forerunner of AlphaZero and was trained on a smaller sample of data than Stockfish, one of the greatest chess engines in the world. In a 100-game contest against Stockfish and Elmo, AlphaZero prevailed by winning 28 games and drawing the remaining 72. The unusual playing style of AlphaZero was also recognized, with a propensity for sacrifice attacks.

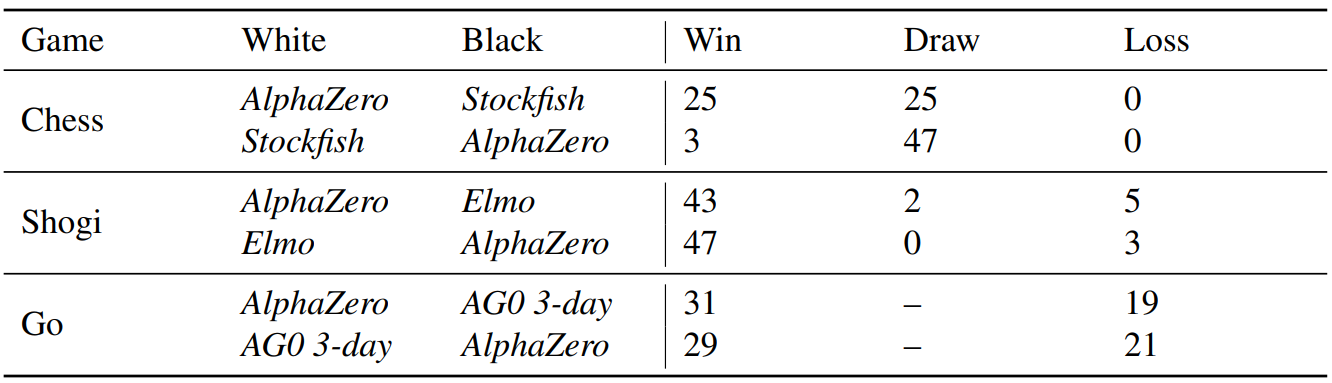
The authors evaluated AlphaZero’s performance in shogi against the top human players and the YSS algorithm, the most powerful shogi program. In a contest of 100 games, AlphaZero defeated the YSS algorithm by winning 90 of them and drawing the remaining ten. The top human players were also used to compare AlphaZero’s performance, and it was discovered that AlphaZero’s style of play was distinct from both the human and YSS styles.

Overall, the study offers a substantial advance in artificial intelligence and shows how well a broad reinforcement learning algorithm works for teaching players how to play challenging games. According to the authors, the technique might be used for other games and fields, such as robotics and optimization issues.

Methodology

Deep Pepper Summary

The Deep Pepper paper adapts methods from AlphaZero, deep networks and monte carlo tree search algorithms. It implements a neural network (value network) to predict state values and the optimal move (policy network) at any state using custom feature representation. This policy network is used together with an MCTS algorithm, and the optimal move is decided by an upper confidence tree selection process. Training is done by embedding some prior knowledge of chess, and using stockfish to early stop the games for an accelerated training.

Deep Pepper uses MCTS for both policy evaluation and policy improvement.There are three main phases of the algorithm (each board state is stored as a node:

1. Selection: The most promising child node for each root node is considered until we come across an unvisited node.
2. Expansion and evaluation: This leaf node is expanded using the neural network, giving the probabilistic values for all possible board moves, and the value of the leaf, ‘v’ is found out using the value network.
3. Back up: The statistics (action values and the number of times the move has been taken) of each explored move is updated

Each node contains N(s, a) (number of times each of its children were visited), W(s, a) (The total value of all descendent leaf nodes as per the value given by the neural network), Q(s, a) (the average value for each node =W(s, a)/N(s, a) ) and P(s, a) (the initial move probabilities that the neural network provides), with Dirichlet noise added to favour exploration. The states and actions are explored using a variant of Polynomial Upper Confidence Tree’s (PUCT), based on estimates on the upper bound of selection probabilities U(s, a) having an exploration factor Cpuct, and the child node is selected as the one that maximises the sum of Q(s, a) and U(s, a).

At the end of each iteration (800 simulations of MCTS), MCTS provides a policy to be used in the current game state. The policy is given by: π(s, a) = N(s, a)/Σa N(s, a)

STATE REPRESENTATION: Complete board representation in the form of 8x8x73 poses certain issues, like having too many layers makes it harder and more time consuming to train,and CNNs can’t be trained to predict sudden changes in output to considerably small changes in input. In light of this, we take inspiration from the Giraffe paper, having a custom 353-dimensional feature vector, which also gives favorable results during pre-training. We also use stockfish embedded knowledge to accelerate training.

NEURAL NETWORK ARCHITECTURE: Multiple architectures are experimented:

1. PolicyValNetwork-parts: The global features are connected to h1a neurons, the piece centric features to h1b neurons and square centric features to h1c neurons in the first layer. All the concatenated outputs from the first layer are then connected to the h2p and h2v neurons in the second layer which give us the policy output and the value function respectively.
2. PolicyValNetwork-Full: Instead of having distinct connections in the first layer, we have a fully connected layer allowing the network to learn more implicit connections between each of the features. An insignificant improvement in performance as compared to the increased training time is observed.
3. PolicyNetwork-parts and Critic-parts: A minor improvement in performance is observed if we also train the first layer independently for policy and value networks (separate).
4. PolicyNetwork-full and Critic-full: very slight improvement in performance

TRAINING ALGORITHM PIPELINE: The training procedure can be viewed as a CAPI. MCTS is used for game generation and improvement testing.

1. Game generation phase: During this phase, deep pepper plays many games against itself. The current board state is used as a root node and the optimal policy is determined. After k half moves,in order to accelerate training, stockfish evaluation is used to indicate the probability for the player to win or lose, resulting in the player/opponent to resign
2. Network training phase: The data is created during the game generation phase as a triplet of: {s, π(s, a), ν}, where s is the board state, π(s, a) is the policy calculated by MCTS, and v is the end game value determined by a draw, win or resignation. The network is trained via back propagation with gradient updates calculated using an Adam optimizer on mini-batches.
3. Improvement Testing phase: an optional check to ensure that the new network has improved over the last iteration. Should the updated network defeat the older iteration by more than half the time, the newly trained network is kept and used in the next round of game generation.

PRETRAINING: An optional phase added in order to offer early guidance in network training.

Stockfish assigns values to the board positions taken from professional chess games, helping us to generate an approximate policy label. This is because training of the policy network doesn’t work directly on expert games. Then, supervised learning is used to train the networks using the generated labels.

The Best Chess Engines

Background

Stockfish chess engine was released in 2008, which was made by open-source developers. It is derived from Glaurang, an open-source engine which was developed in 2004. This chess engine was the strongest chess engine and had won many chess matches.

In 2017, DeepMind, which is a subsidiary of Google, developed a chess engine, named AlphaZero, which defeated Stockfish multiple times and shocked the chess community. In Stockfish, the approach is to use sophisticated search techniques, domain-specific adaptations, and handcrafted evaluation functions that have been refined by human experts over several decades.

But in AlphaZero, the only input given to it was rules of chess. It uses a deep neural network for evaluation which is trained by a reinforcement learning algorithm. This engine has also worked successfully on games like Shogi and Go.

Stockfish

Stockfish uses handcrafted features which consists of : Mobility or Trapped Pieces, Pawn Structures, King’s Safety, number of pieces left, outposts etc. Each of these features has a specific weight assigned to it and evaluation of a position is resulted from the sum of features multiplied to its respective weights. For evaluating a position, stockfish spans a tree of possible ways to move and evaluates using the evaluation function. The problem is that the size of complete chess tree could go to near 10123, and evaluating that would be difficult. So we limit the breadth and depth of search by using Alpha-Beta algorithm. This algorithm tries to go through the search which drops the worst options for the other player, instead of finding the highest value of search evaluation. This approach works best if we consider the best moves as early as possible. For example, if we conduct a search of all moves in ascending order, we would have to go through all possible positions. But if we consider strongest move first, then the algorithm would reduce the node that has to be evaluated to its root (if x is number of node, it will reduce it to ). Stockfish uses an opening book to choose moves in the first phase of the game as well an endgame tablebase that includes the best moves for all positions with six or less pieces left on the board

AlphaZero

In the case of AlphaZero, instead of using handcrafted features for evaluation function, it uses a deep neural network which is trained by reinforcement learning.

In this algorithm, the first step is to choose the initial position from where it should start and then to decide what moves it should make. The input to the neural network is all 64 squares in the chess board and all the move possibilities each piece would have on each of these squares. As each square is treated in the same way, it leads to certain illegal moves, which is then rectified by the chess rule which is given input to the engine by reducing their probability to zero. The output from this neural network is a vector containing 2 values. One signifies the percentage of search time and another is the win probability that the neural network assigns to this move. The training of this neural network is done by making it play with itself. The neural network is trained by Monte-Carlo Tree Search algorithm.

Results and Improvements

Monte Carlo Tree Search Accuracy:

The accuracy of Monte Carlo Tree Search (MCTS) refers to the algorithm’s capacity to accurately predict the outcome of future moves in a game of chess. It depends on several factors such as the accuracy of the evaluation function used to estimate the value of a game position and the number of simulations performed by the algorithm. It is crucial in determining the effectiveness of the moves made by the AI agent. Poor accuracy can result in the agent performing poorly and making bad decisions. As a result, one of the key objectives of this project is to increase MCTS accuracy.

Cyclic Learning Rates:

Cyclic Learning Rates (CLR) is a technique used in reinforcement learning to tune the learning rate hyperparameter. The learning rate, in a conventional approach, is manually established and remains constant over the course of the training. However, this fixed learning rate may not be appropriate for different phases of the training process, which can result in suboptimal results.

Cyclic Learning Rates vary the learning rate over multiple cycles, by initially starting with a low learning rate and gradually increasing it to a maximum value before lowering it once more. Throughout the training phase, this cycle is repeated numerous times.

The main advantage of doing this is that the learning rates adapt to the dynamics of the training process and avoid getting stuck in local optima. They encourage the model to move out of the local minimum and instead identify the global one by periodically raising the learning rate.

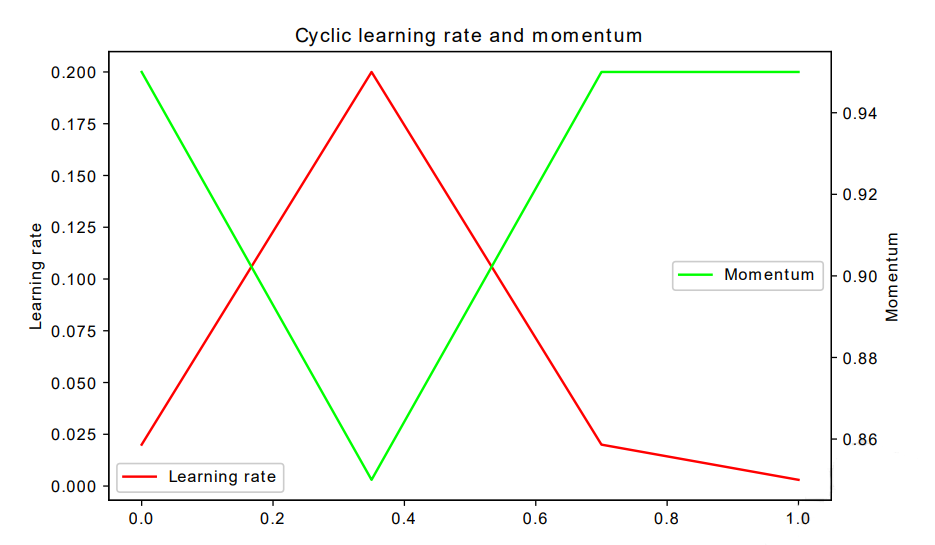
This figure shows how the learning rate and momentum is varied every iteration. It can also be noticed that the change in learning rate is minimal towards the end of training to accommodate the fact that the policy shouldn’t change too much towards the end.

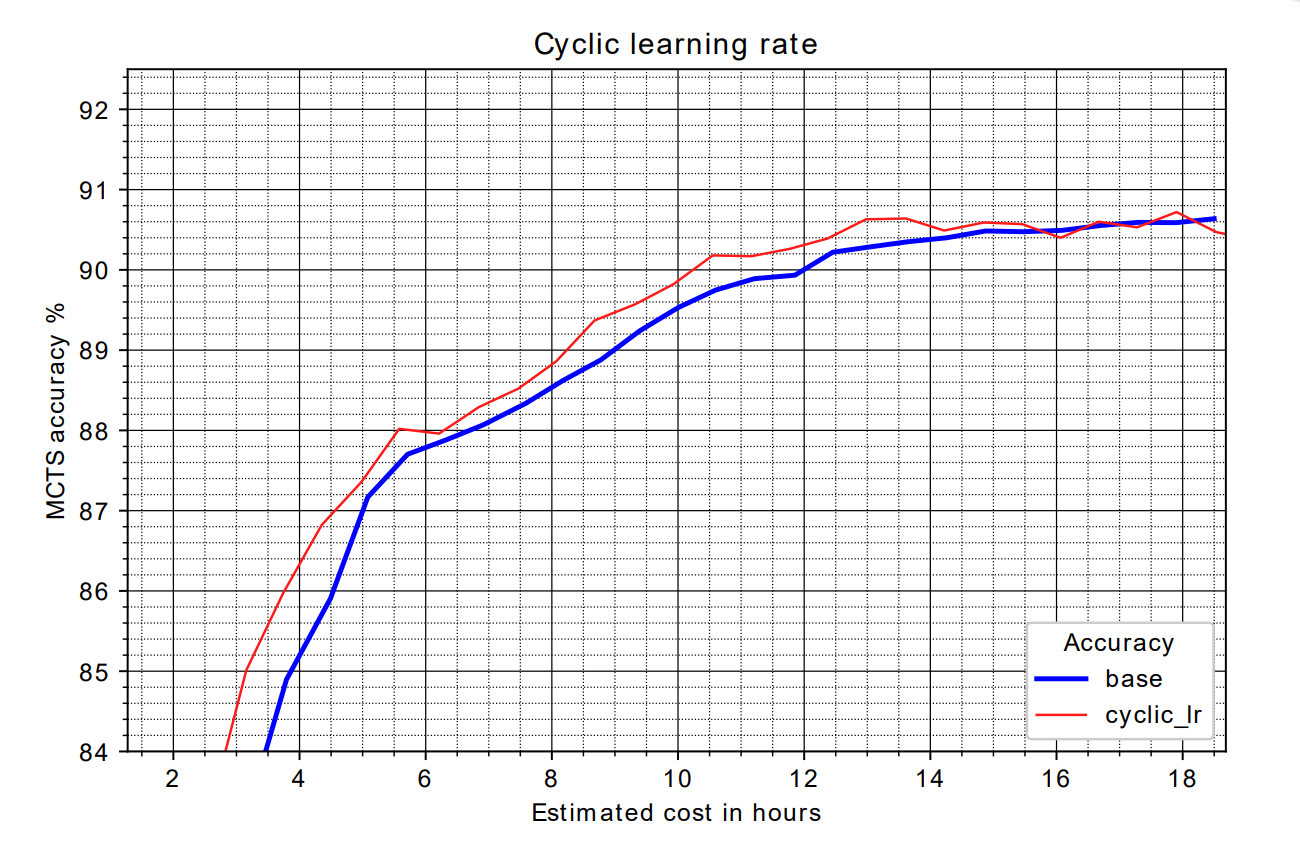
This figure shows the MCTS accuracy with and without cyclic learning rates. It can be seen that initially the model using cyclic learning rates has a higher accuracy but towards the end the difference is negligible.

Squeeze and Excite:

Squeeze and Excitation (SE) is a technique that can be used to improve the performance of convolutional neural networks (CNNs). It aims to capture the interdependence between channels by learning a channel-dependent weighting mechanism, which dynamically adjusts the channel activations based on their importance.

The squeeze operation and the excitation operation are the SE module’s two main parts. In order to capture the global information for each channel, the squeeze operation decreases the spatial dimension (H x W) of feature maps to a single dimension. The excitation operation is in charge of learning a channel-wise weighting mechanism, which determines the significance of each channel at each point.

The chess engine’s performance can be enhanced by including the SE module in its CNN architecture. It can be used to extract high-level features from the input data following a convolutional layer. The data from all channels are then combined into a vector via the SE module’s squeezing of the feature maps along the channel dimension.

The excitation operation follows, which learns a set of parameters to model the dependencies between various channels in the feature maps. A weighted vector is created as a result, capturing the significance of each channel. Finally, the feature maps are obtained by multiplying the weighted vector with the original feature maps.

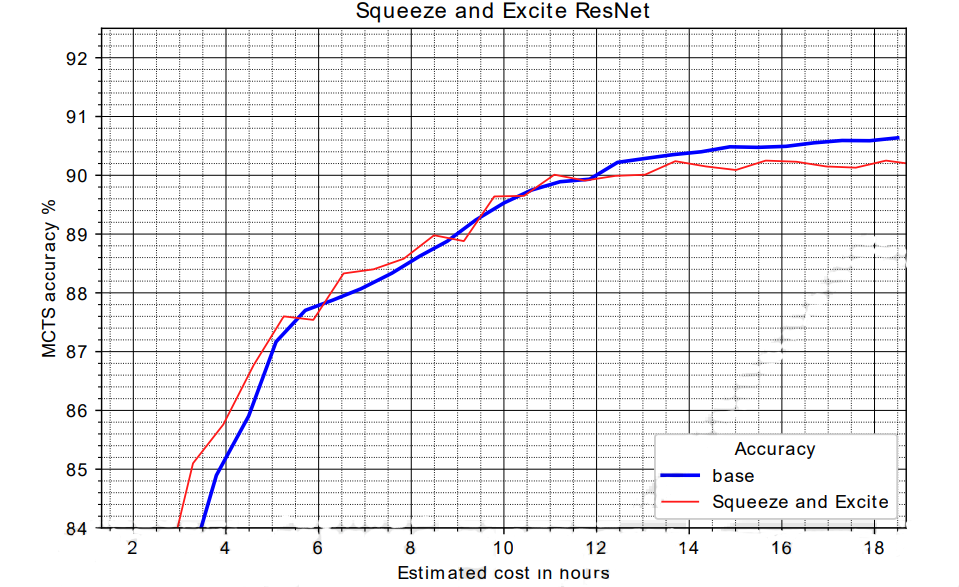
This figure shows the MCTS accuracy trends with and without Squeeze and Excite. It can be seen that there are some early gains early during the training but there some losses later on. Overall, it does not affect the performance much and intuitively it should help.

C-PUCT:

C-PUCT extends the traditional MCTS algorithm by adding continuous progress estimates, which allow the algorithm to better allocate computational resources and improve search efficiency. To determine the optimum moves, it uses an Upper Confidence Bound (UCB) method with the additional benefit of updating the confidence bounds in real time while the search goes on.

The C-PUCT algorithm can be used in a chess engine to find the best move by searching through the possible move sequences from the current position on the chessboard. The algorithm can reduce the search space and quickly determine the optimum move by using a search tree and a combination of deterministic and probabilistic heuristics.

The quality of the input features used and the precise algorithmic parameters chosen will determine the move that the C-PUCT algorithm generates. To get the chess engine to function at its best, these parameters typically need to be adjusted.

Conclusion

The observation of a limited application due to the significant hardware demands in this research spurred the need for effective and scalable improvements of Deep Pepper. Cyclic Learning Rates showed great potential while other methods like Squeeze and Excite and Hyperparameter Tuning showed decent increase in performance too. Overall, the hardware demands were reduced and the performance of the model was increased with these improvements.

Bibliography

1. Deep Pepper: Expert Iteration based Chess agent in the Reinforcement Learning Setting https://arxiv.org/pdf/1806.00683.pdf
2. Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm https://arxiv.org/abs/1712.01815
3. Giraffe: Using Deep Reinforcement Learning to Play Chess https://doi.org/10.48550/arXiv.1509.01549
4. Supervised and Reinforcement Learning from Observations in Reconnaissance Blind Chess https://doi.org/10.48550/arXiv.2208.02029
5. Reinforcement Learning in an Adaptable Chess Environment for Detecting Human-understandable Concepts https://doi.org/10.48550/arXiv.2211.05500