The following work was carried out during my summer internship at the Multi-Agent Robotic Motion Laboratory, National University of Singapore under the supervision of Dr. Guillaume Sartoretti.
Hybrid PPO
Hybrid Proximal Policy Optimization (Hybrid PPO) is an innovative actor-critic algorithm designed for learning in a parameterized action space. The key feature of H-PPO lies in its utilization of parallel actors, where discrete and continuous action selection are performed independently. This architecture decomposes the complex action space into simpler components, enhancing the learning efficiency of the model. The algorithm employs a global critic network to update the policy parameters of both the discrete and continuous actors.
H-PPO operates in a parameterized action space, allowing the agent not only to select discrete actions but also to choose continuous parameters associated with those actions. This flexibility enables the model to make nuanced decisions, crucial for tasks with intricate action requirements.
Architecture
Parallel Actors:
- Discrete Actor Network (πθd): Learns a stochastic policy for discrete actions. It outputs k values fa1 , fa2 , . . . , fak for the k discrete actions, and the discrete action ‘a’ is randomly sampled from the softmax(f) distribution.
- Continuous Actor Network (πθc): Learns a stochastic policy for continuous parameters associated with discrete actions xa1 , xa2 , . . . , xak. It generates the mean and variance of a Gaussian distribution for each parameter.
The complete action to execute is the selected action a paired with the chosen parameter xa corresponding to action a. The two actor networks shares the first few layers to encode the state information.
H-PPO incorporates a single critic network (V(s)) that estimates the state-value function. Using the state-value function instead of the action-value function mitigates over-parameterization issues in the parameterized action space.
The discrete policy πθd and the continuous policy πθc are updated separately by minimizing their respective clipped surrogate objective.
The probability ratio rtd (θd) only considers the discrete policy and rtc (θc) only considers the continuous policy. Even though the two policies work with each other to decide the complete action, their objectives are not explicitly conditioned on each other. πθd and πθc are viewed as two separate distributions instead of a joint distribution.
Rewards
In traffic signal control, the choice of reward functions plays a pivotal role in shaping the behavior of reinforcement learning-based approaches. We investigate two prominent reward strategies: Max Pressure (MP) and Intensity-based Proximal Dynamic Adaptive Light (IPDALight). While MP prioritizes throughput and congestion minimization, IPDALight introduces a nuanced perspective by considering detailed vehicle dynamics, such as speed and position, to enhance traffic signal control policies.
Max Pressure (MP) Control
The objective is to minimize intersection pressure defined as the difference between the number of vehicles on incoming and outgoing lanes.
Strengths:
- Throughput Maximization: MP aims to maximize the flow of vehicles through intersections, optimizing for high throughput.
- Simple and Effective: Known for its simplicity, MP often yields effective solutions for reducing congestion and delays.
Limitations:
- Locally Optimal Solutions: MP can be greedy, leading to locally optimal solutions that may not be globally efficient.
- Lack of Vehicle Dynamics: The method does not consider vehicle dynamics, ignoring factors such as speed and position.
IPDALight: Intensity-based Proximal Dynamic Adaptive Light
The objective is to minimize the intensity of intersections, considering detailed vehicle dynamics, including speed and position.
Features:
- Intensity Calculation: Considers the speed, position, and distance of vehicles approaching an intersection to compute intensity.
- Logarithmic Scale: Mitigates the impact of large product values, offering a more balanced intensity metric.
- Dynamic Phase Duration: Proposes a heuristic to fine-tune phase duration based on dynamic traffic situations.
Intensity of vehicle increases when it approaches an intersection or the speed decreases due to traffic congestion. $(L-x)/L$ shows the impact of distance on intensity: closer the vehicle is to the intersection, greater is the intensity. The other term indicates the impact of slower vehicles on intensity. So by definition, vehicles crossing an intersection with higher speed will pose lower intensity on the intersection.
Intensity of Lanes: sum of intensity of all vehicles on the lane.
\[\mathcal{T}_{\text {lane }}=\sum_{\text {veh }_i \in \text { lane }} \mathcal{T}_{\text {veh }_i}\]Intensity of Intersections: It is the intensity difference between the incoming lanes and the outgoing lanes. It evaluates the overall traffic pressure suffered by the intersection.
\[\mathcal{T}_{\mathcal{I}}=\sum_{\text {lane }_i \in \text { lane }_{\text {in }}} \mathcal{T}_{\text {lane }_i}-\sum_{\text {lane }_j \in \text { lane }_{\text {out }}} \mathcal{T}_{\text {lane }_j}\]Reward definition - The intensity of intersections reflects the average travel time of vehicles crossing the intersection more accurately than the MP-model because it considers more vehicle dynamics. So their reward is $r$ = $-$(Intensity of $I$)
Advantages:
- Accurate Representation: Reflects average travel time more accurately by considering detailed vehicle dynamics.
- Adaptive Phase Duration: Provides a heuristic to adjust phase duration, adapting to changing traffic conditions.
Challenges:
- Complexity: The inclusion of detailed vehicle dynamics adds computational complexity compared to MP.
- Implementation Challenges: Fine-tuning phase duration requires careful implementation and real-time adaptation mechanisms.
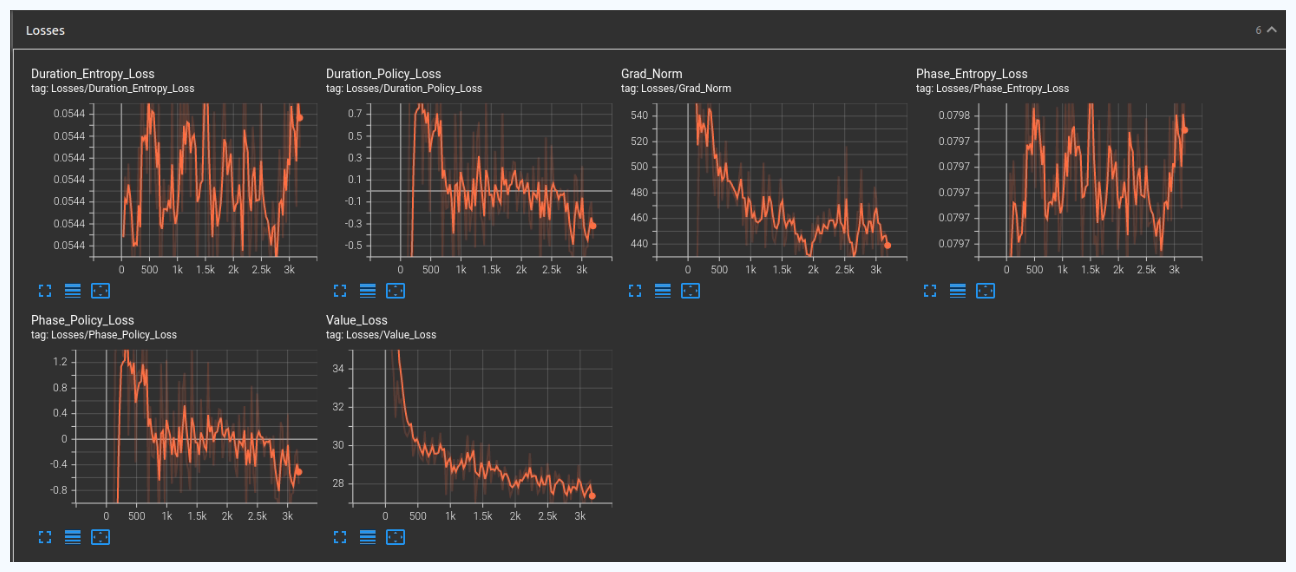
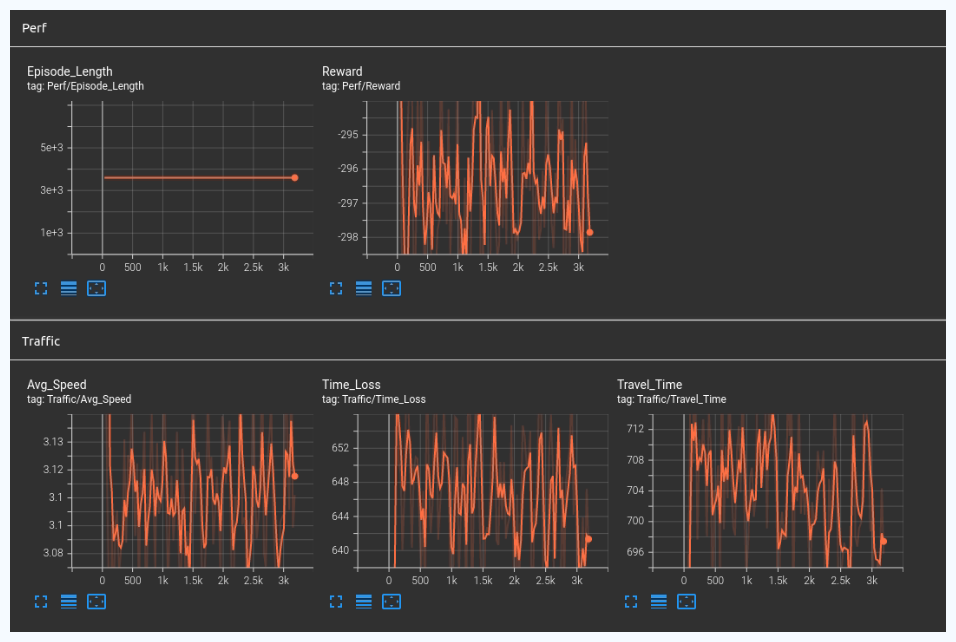
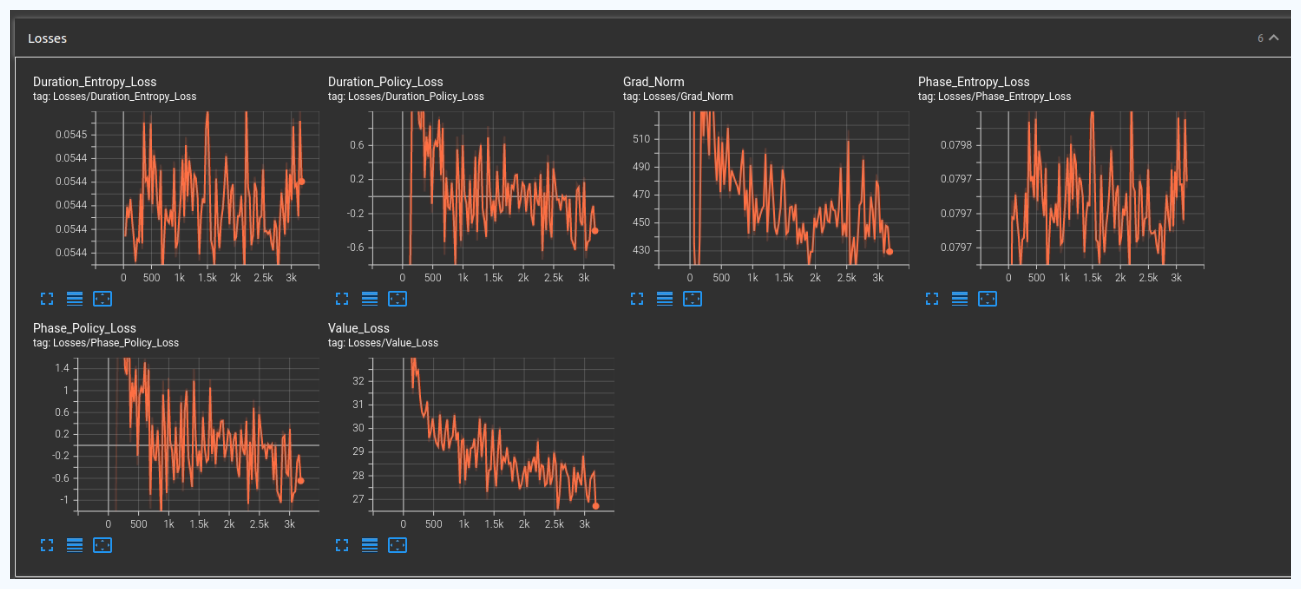
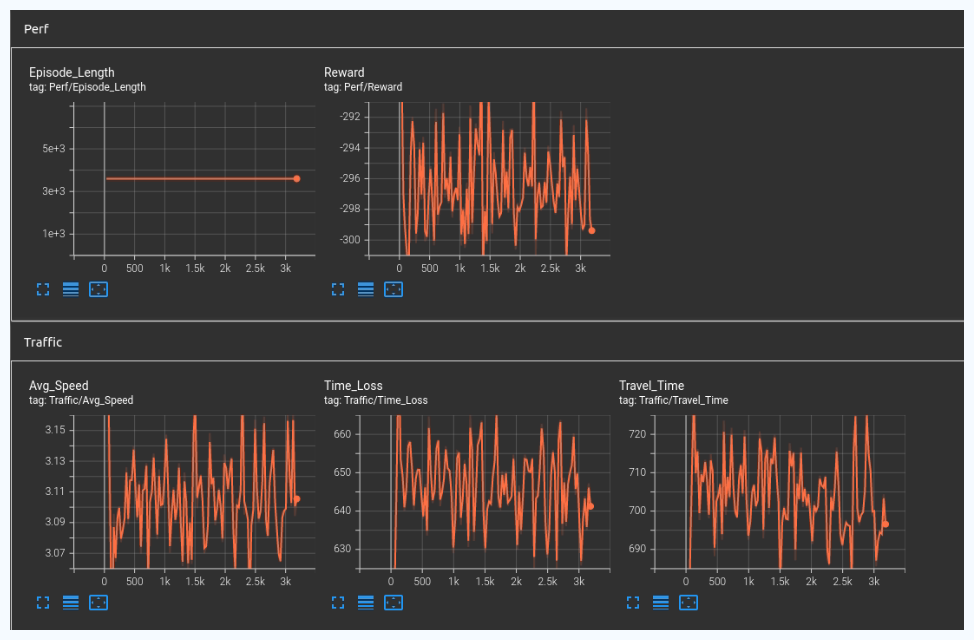
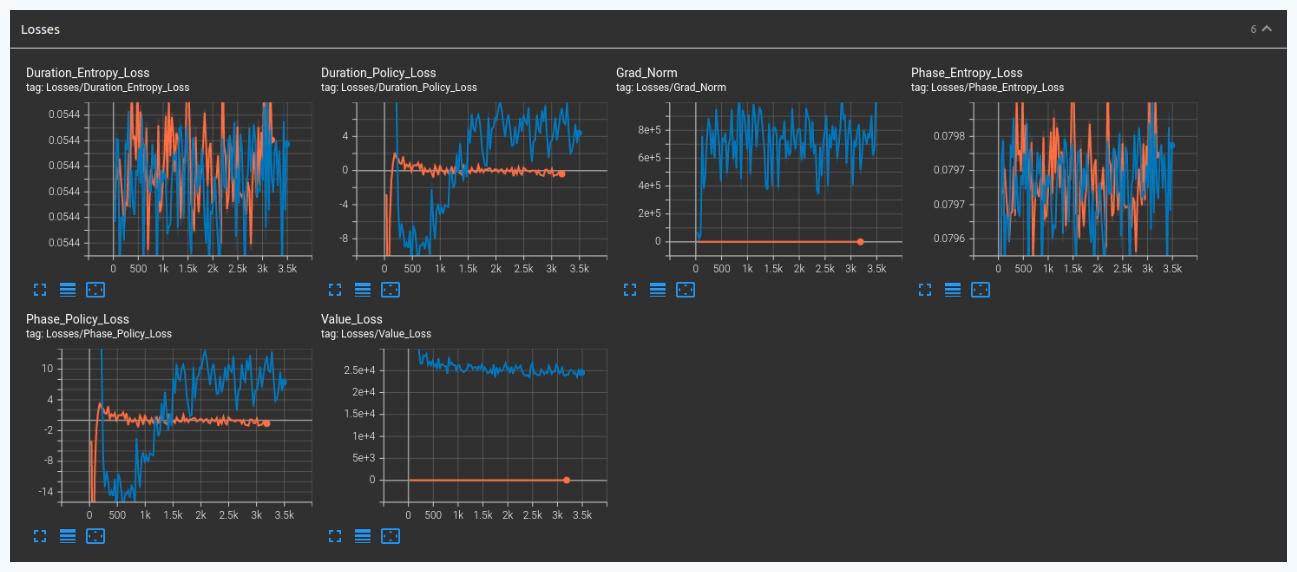
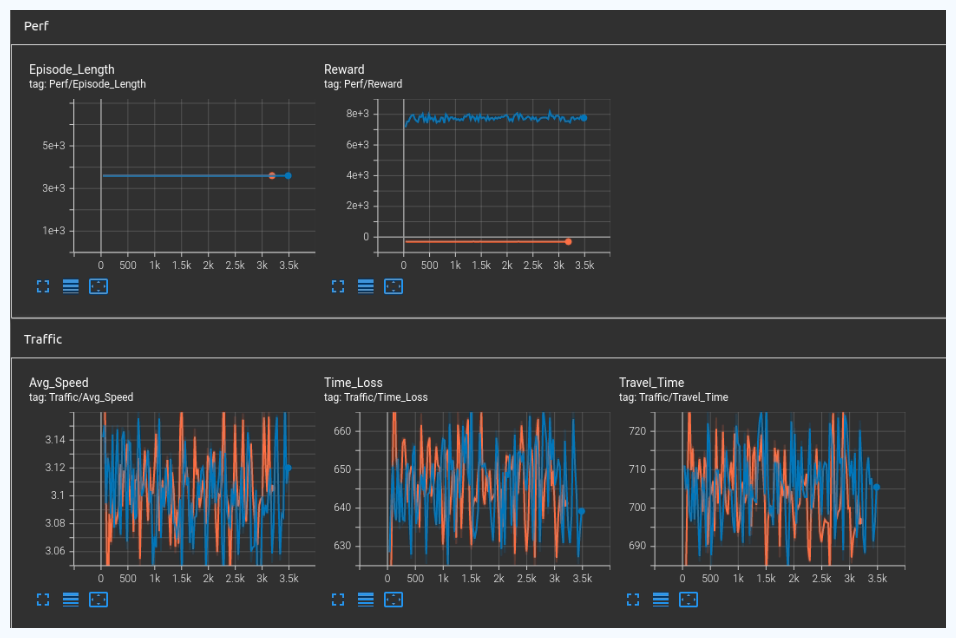
Results